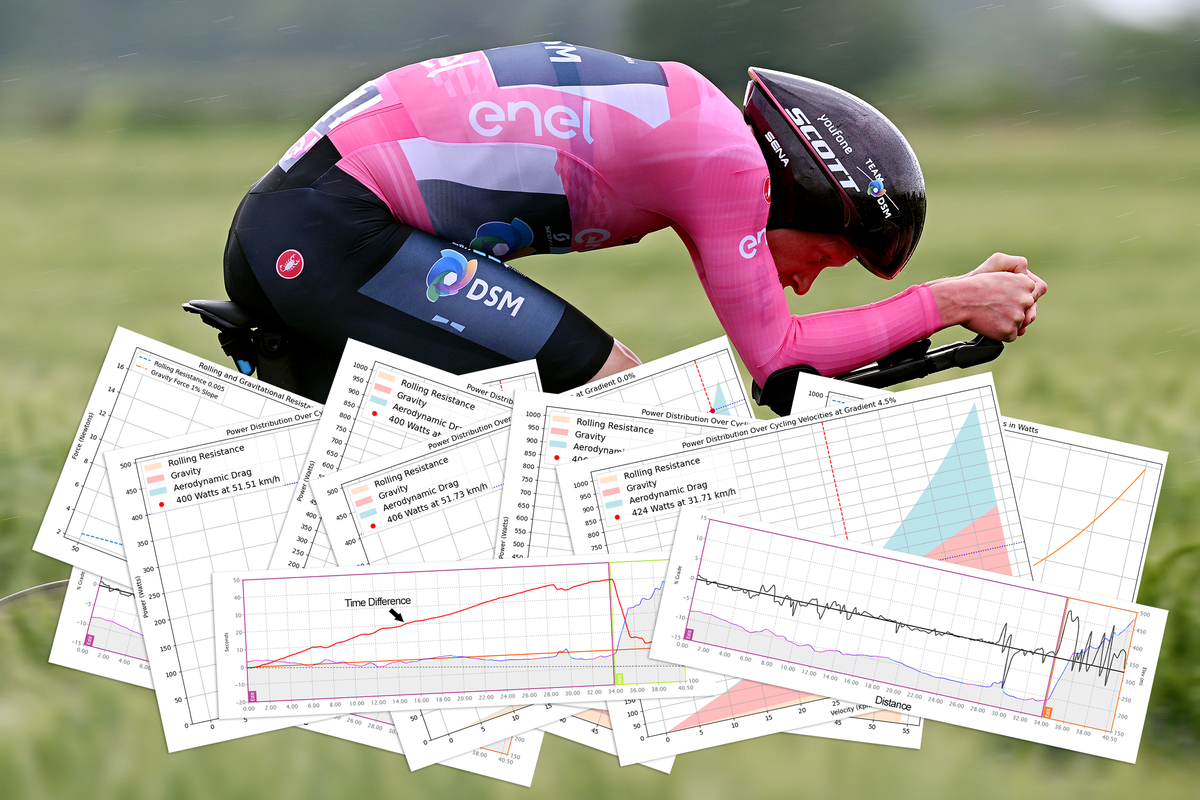
Calcul de la stratégie de rythme, de la stratégie d'échange de vélo, de la dépense énergétique et plus encore
Comment optimiser pour un contre-la-montre Grand Tour ? Le parcours de contre-la-montre du Giro d'Italia 2024 avec un dénivelé de 420 mètres est l'arène idéale pour se plonger dans le geek de la performance du contre-la-montre. Notre premier défi est d’optimiser notre temps avec une stratégie de rythme astucieuse ; nous verrons ensuite si un échange de vélo sera plus rapide pour les pros vendredi ; et enfin, l'étape sera-t-elle une journée pour un homme fort comme Filippo Ganna ou un grimpeur comme Tadej Pogačar ?
L'aspect intéressant du parcours contre-la-montre du Giro de 40,8 km est l'endroit où se situe le dénivelé. Les 33 premiers kilomètres sont relativement plats. Si le parcours devait se terminer au kilomètre 33, le mieux serait simplement d'essayer de conserver votre plus haute puissance durable de Foligno à Ponte San Giovanni. Cependant, notre destination finale est Pérouse, 7 km plus loin, avec des pentes culminant à 16 %.
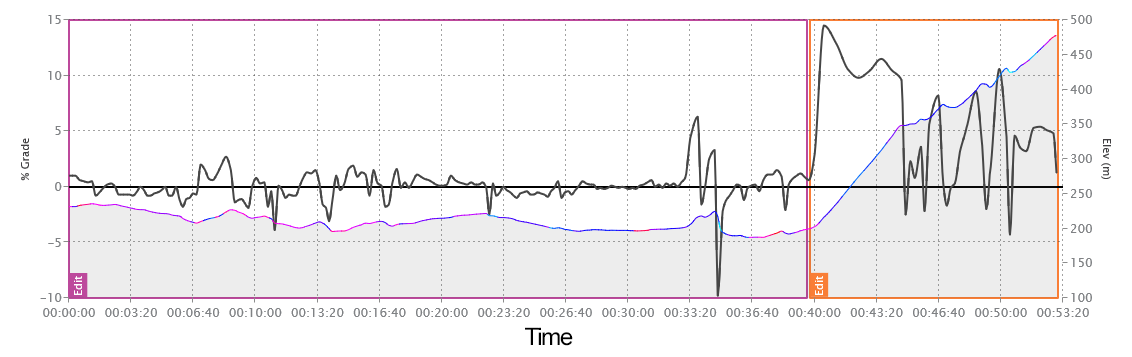
Vous trouverez ci-dessous deux cartes d'élévation. La première est la carte d’élévation traditionnelle, avec la distance le long de l’axe X. Le deuxième graphique montre un temps de simulation le long de l'axe X, révélant l'importance de ces 7 derniers kilomètres du parcours.
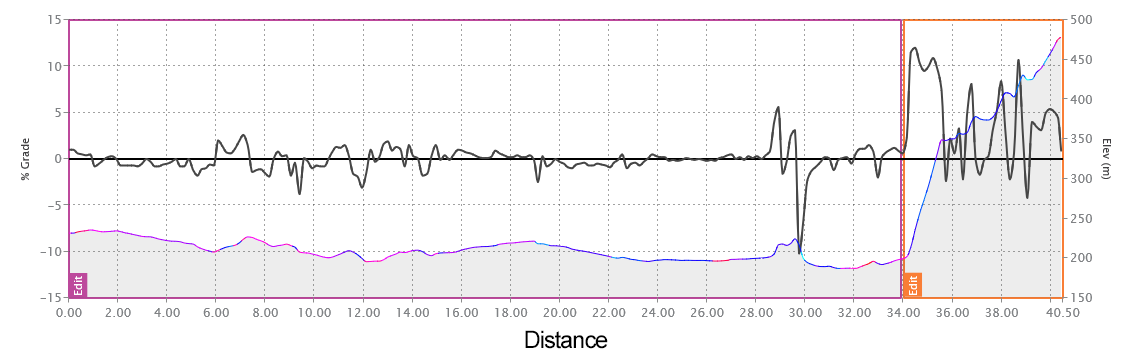
Passons maintenant à notre défi, optimiser notre puissance de sortie pour ce cours. Imaginez que nous sommes un cycliste professionnel participant au contre-la-montre individuel du Giro d'Italia. Notre puissance cible pour le contre-la-montre individuel est d'environ 400 watts (~1300Kj). Nous choisissons d'attribuer un « budget » supplémentaire conservateur de 20 Kj pour optimiser la stratégie énergétique. J'expliquerai bientôt pourquoi un budget serait décidé de cette façon.
Nous pouvons soit :
- Rythmez uniformément notre contre-la-montre en répartissant les kilojoules sur les 40 km
- Dépensez tous nos kilojoules supplémentaires sur le dernier secteur en montée de 7 km.
Tout d’abord, qu’est-ce qu’un kilojoule et pourquoi budgétiser notre énergie de cette façon et non en watts ? Un kilojoule est une mesure d'énergie. Un watt équivaut essentiellement à un joule par seconde. Ainsi, pour déterminer à combien de watts équivalent nos 20Kj, nous devons diviser nos kilojoules par la durée en secondes. En distribuant de l'énergie plutôt que des watts, nous pouvons être sûrs de donner à chacun de nos plans de stimulation une course virtuelle équitable.
Watts = Kj*1000 / durée en secondes
Commençons par examiner comment l'énergie est distribuée lorsque l'on fait du vélo. Cela pourrait nous donner une idée de la meilleure façon de dépenser notre budget.
Premièrement, nous devons faire face aux pertes de transmission. Partout où deux pièces mobiles se rencontrent, il y a une perte par friction. Les transmissions les plus efficaces fonctionnent avec des pertes de 2 %, alors qu'une transmission standard bien entretenue sera d'environ 3 %. Cela signifie qu'un cycliste roulant à 200 watts avec une transmission standard dispose d'une puissance nette de 194 watts contribuant à la propulsion du vélo.
Ensuite, je trouve qu'il est logique de diviser les forces restantes agissant contre nous lorsque nous cyclons en deux catégories, les résistances affectées par notre masse (poids du système) et la résistance de l'air. Vous verrez pourquoi cela est utile lorsque je vous montrerai comment les deux se comportent différemment lorsque nous modifions l'entrée de vitesse (vitesse) dans nos formules.
Dans notre catégorie « résistances affectant la masse », nous avons la gravité et la résistance au roulement. Monter une côte nécessite évidemment un effort plus important à mesure que nous augmentons notre masse en raison de la gravité, mais l'effet parfois négligé de la masse concerne la résistance au roulement des pneus.
La résistance au roulement a un coefficient. Il s'agit d'un rapport qui décrit la force nécessaire pour vaincre la masse de charge verticale sur le pneu. Généralement, un bon pneu de vélo de route se situe entre 0,004 et 0,005. Plus le coefficient est élevé, plus la force requise pour la même vitesse est grande.
Jetez un œil à la façon dont l’augmentation de la masse affecte les deux résistances.
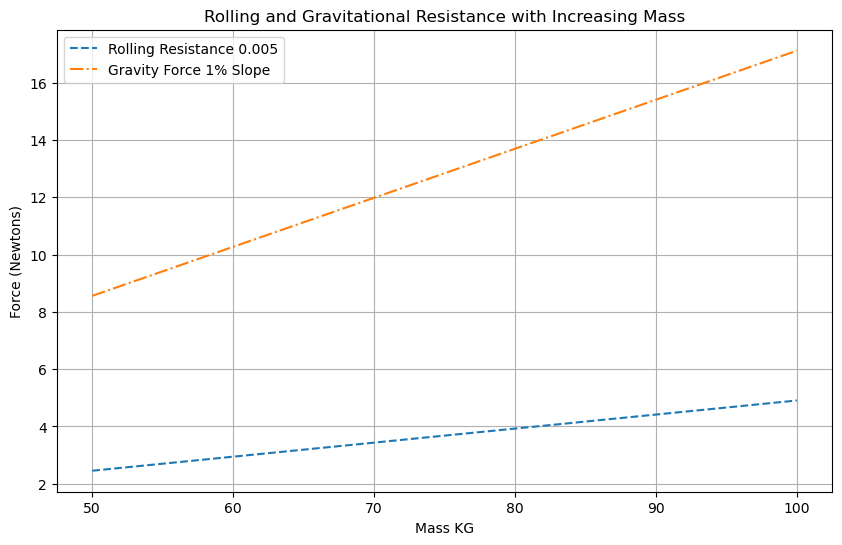
Watts de roulement = Coefficient de roulement * Gravité * Masse * Vitesse
Gravité Watts = Masse* Gravité * sin(Pente) * Vitesse
La résistance de l’air est ce que nous appelons une force exponentielle. Le graphique suivant montre comment la résistance de l'air réagit à l'augmentation de notre vitesse. Remarquez qu'il ne serait pas facile de tracer cette ligne avec une règle.
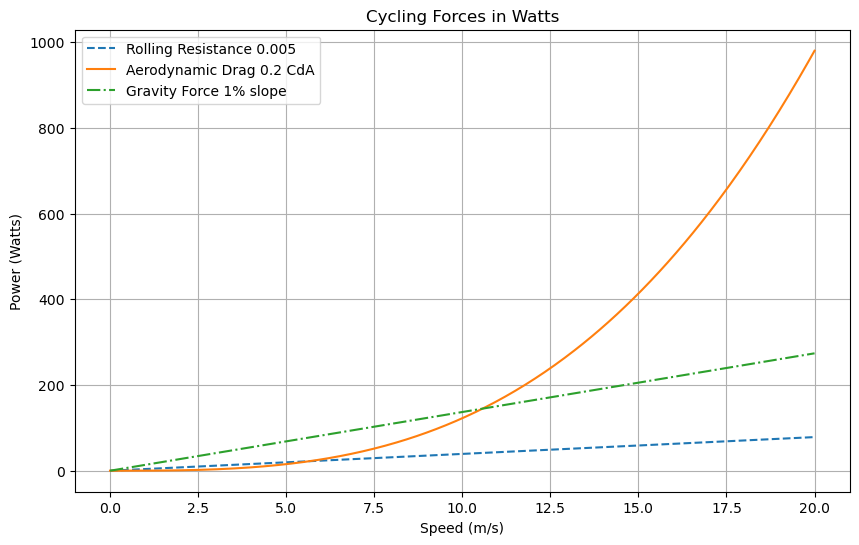
La résistance à l’air devient très rapidement incontrôlable par rapport à nos résistances à masse linéaire.
Les entrées pour la résistance de l'air sont la vitesse de l'air, la densité de l'air et notre coefficient de traînée (CdA). Notez que nous utilisons la vitesse air et non la vitesse sol.
Air Watts = 0,5 * Densité de l'air (rho) * CdA * Vitesse de l'air2 * Vitesse
Il y a donc un passage très rapide des résistances que nous devons surmonter pour rouler plus vite. Revenons maintenant à notre défi contre la montre.
Comme nous n'utilisons pas de superordinateur tel que myWindsock.com pour traiter chaque mètre de notre contre-la-montre, y compris la météo, nous devrons simplifier notre parcours en deux sections, un secteur de 33 km à 0% de pente et un secteur de 7 km avec une moyenne. pente de 4,5%.
Jusqu’à présent, nos formules nous donnent la puissance requise pour vaincre la résistance à une vitesse donnée. Notre expérience de stimulation nous oblige à déterminer la vélocité (vitesse). Maintenant, cela devient délicat car vous remarquerez que nous avons besoin de vitesse dans nos équations linéaires et exponentielles (quadratiques). Afin de résoudre nos équations linéaires, nous avons besoin de la réponse à notre équation exponentielle et vice-versa. Pour résoudre ce problème, tracer sur un graphique s’avère pratique.
Vous trouverez ci-dessous nos graphiques pour résoudre nos estimations initiales de la durée. Nous commencerons par une durée de référence pour le secteur plat de 33 km et le secteur final de 7 km en montée. Nous faisons cela afin de pouvoir répartir équitablement notre budget de 20 Kj dans nos deux scénarios sur la durée estimée.
Pour les calculs suivants, nous avons un CdA de 0,2, une résistance au roulement de 0,0044 et le poids (masse) de notre système est de 80 kg..
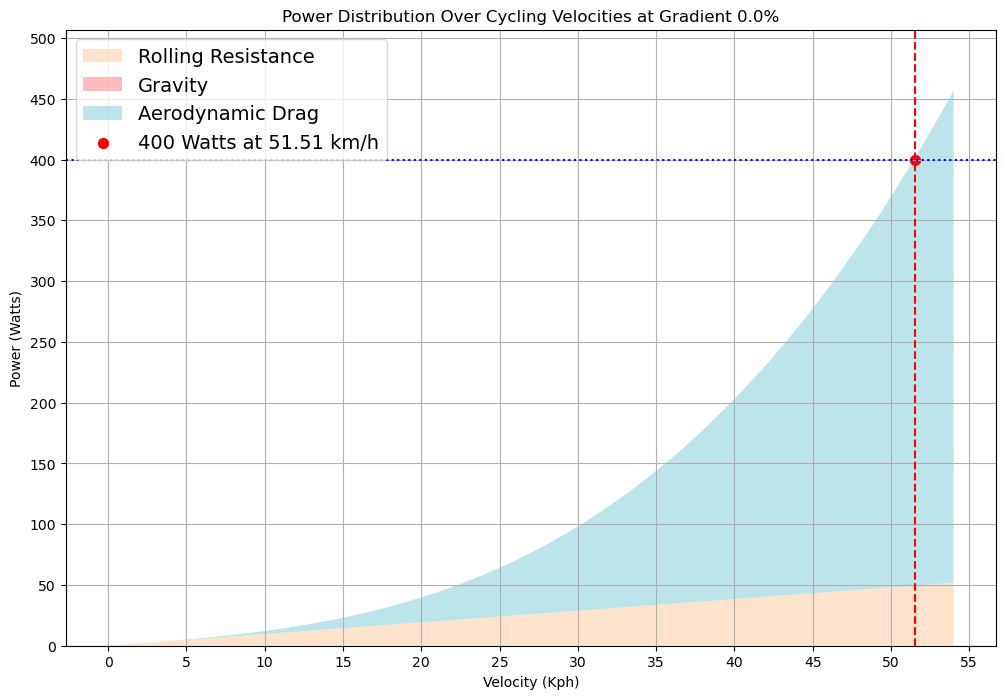
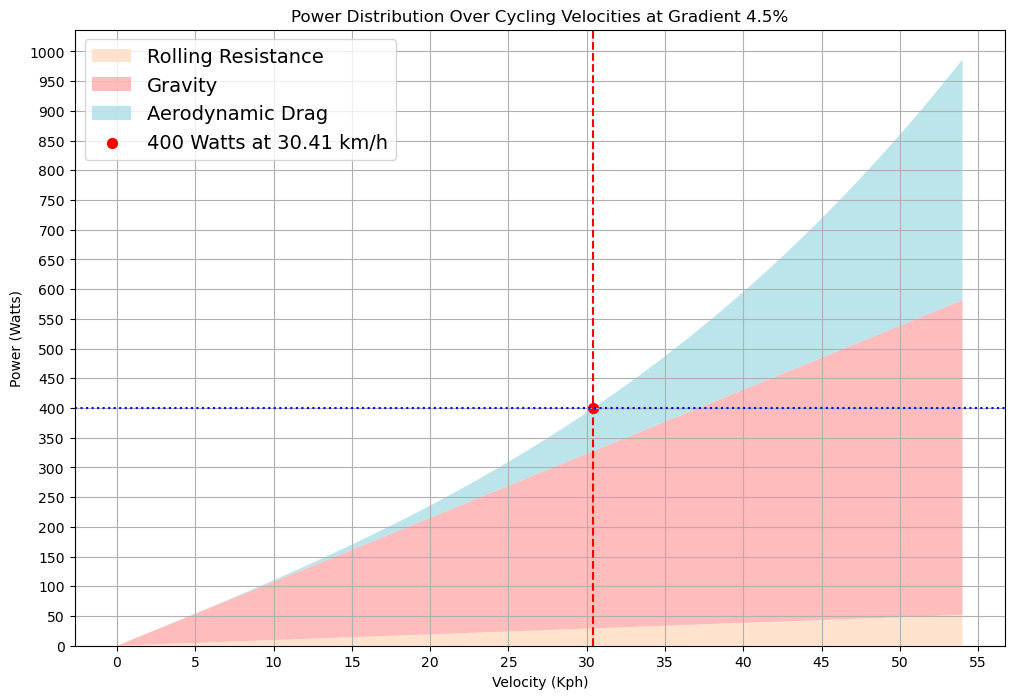
À l’aide des graphiques ci-dessus, nous avons localisé nos estimations de vitesse. Pour obtenir nos durées pour chaque section, nous devons diviser la vitesse par la distance.
Maintenant, nous calculons notre puissance supplémentaire pour notre contre-la-montre au rythme régulier. En divisant nos 20 Kj sur la durée de référence totale de 52 : 13, nous obtenons 6 watts supplémentaires. 52:13 équivaut à 3 133 secondes, et 20 Kj (ou 20 000 joules) divisé par 3 133 équivaut à 6,38 joules par seconde. Par souci de simplicité, nous avons arrondi à 6 joules par seconde, ce qui équivaut à 6 watts.
En utilisant les formules discutées précédemment, générons nos graphiques une autre fois. Cette fois, avec notre ensemble de puissance pour un contre-la-montre au rythme uniforme à 406 watts (400 d'origine plus 6 watts de « budget » supplémentaire)
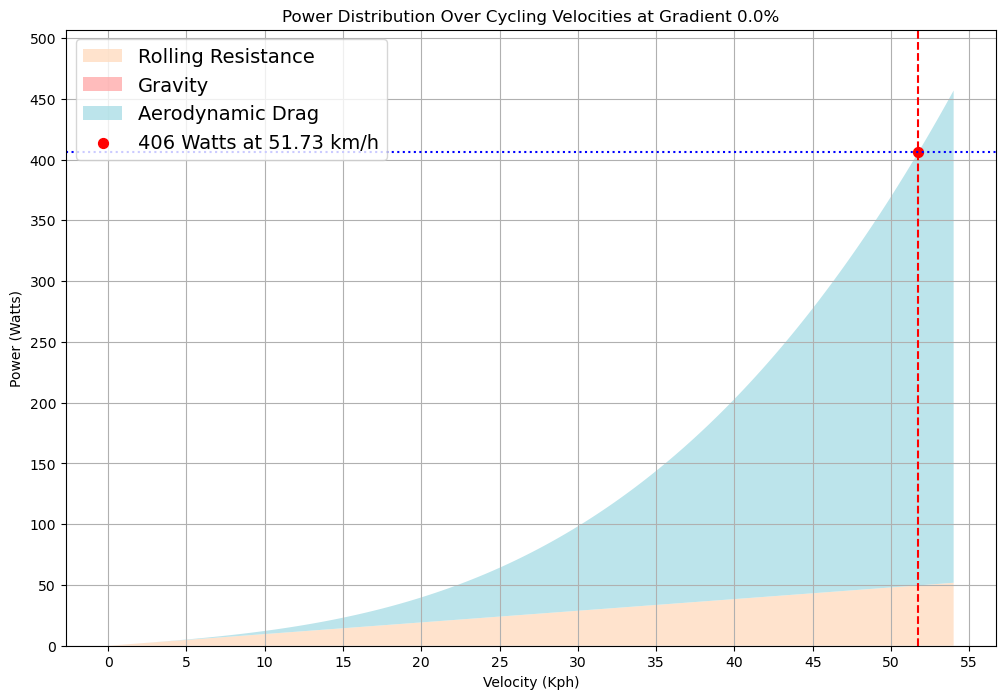
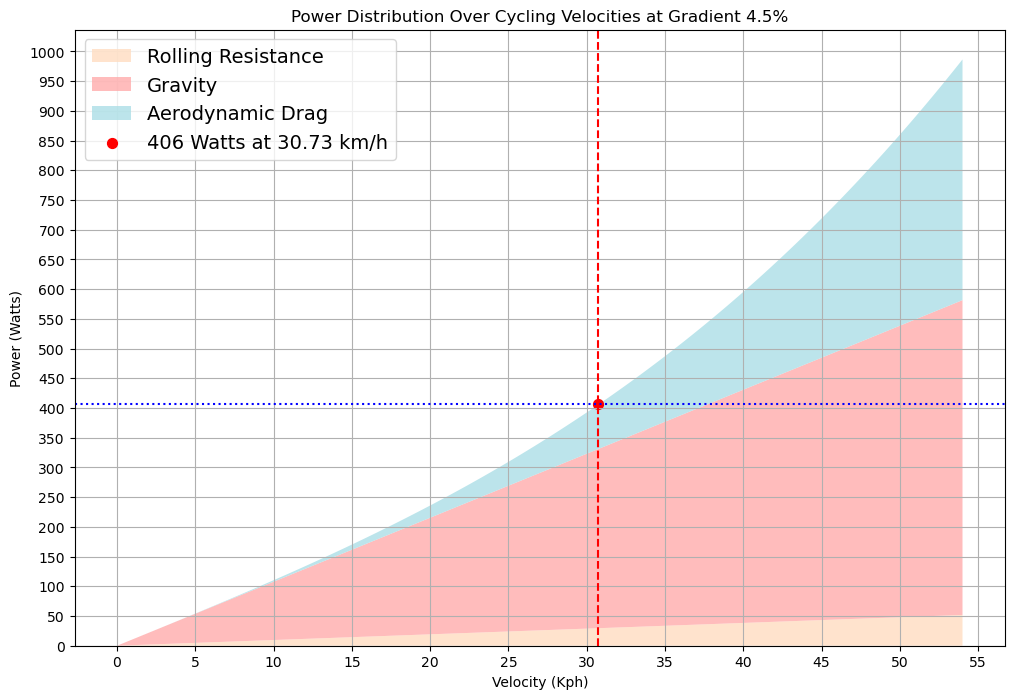
Encore une fois, nous calculons notre temps total de la même manière.
La puissance supplémentaire nous a fait gagner 18 secondes. Ce n’est pas surprenant étant donné que nous avons 6 watts de plus que la puissance de base. Cependant, avez-vous remarqué que le changement relatif de nos vitesses était beaucoup plus important lors de notre dernière montée de 7 km ?
Maintenant, notre budget de 20Kj doit être déployé uniquement dans le dernier secteur en montée de 7 km. Nous revenons à notre heure initiale estimée à 13h47 et divisons nos 20Kj. Cela nous donne 24 watts supplémentaires, ce qui nous amène jusqu'à 424 watts pour la montée. Nous savons déjà que le temps de nos premiers 33 km à 400 watts était de 38 minutes 26 secondes. Mais quels seront nos derniers 7 km ? Faisons le calcul et regardons le graphique.
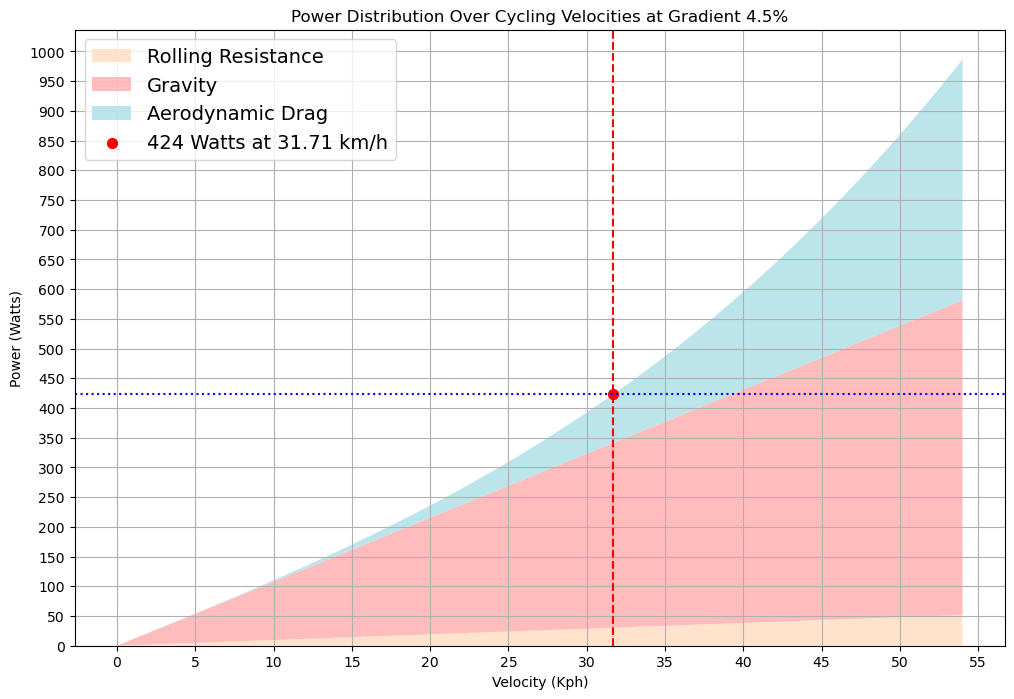
Une dernière fois, nous calculons notre temps total de la même manière.
Pour une même dépense énergétique, nous avons gagné 15 secondes supplémentaires simplement en la répartissant différemment. En fait, ce serait plus que cela car nous avons réduit le temps de notre secteur, ce qui signifie que nous pourrions potentiellement produire encore plus de puissance et être encore plus rapides. Pour faire correspondre parfaitement les kilojoules, nous devrons à nouveau effectuer plusieurs itérations pour respecter notre marge d'erreur acceptable.
Bien entendu, le parcours actuel du Giro présente des dénivelés variables. À mesure que le gradient augmente, l’efficacité de notre puissance supplémentaire augmentera.
Pourquoi sommes-nous plus rapides lorsque nous appliquons notre puissance supplémentaire au secteur ascendant ? Revenons à ces équations linéaires et exponentielles. À mesure que la résistance de l’air augmente, notre rendement pour chaque watt diminue, comme le démontre la courbe exponentielle. Alors que les forces linéaires, la gravité et la résistance au roulement, ont un retour entrée-sortie beaucoup plus favorable.
Dans l’attente de l’étape 7 du Giro, que révèle notre geekery du contre-la-montre ? Pour les informations suivantes, nous devons prendre en compte tous les rebondissements, les pentes et les déclins ainsi que l’évolution des conditions météorologiques.
Pour ce faire, j'utilise le simulateur alimenté par l'IA, myWindsock.com.
Un échange de vélo aurait-il du sens ?
Nous avons déjà étudié le fait que dans les 7 derniers kilomètres jusqu'à Pérouse, la pente moyenne est de 4,5 %. Mais cela ne raconte que la moitié de l’histoire. Pour les premiers 1,5 km, la route atteint en moyenne 10 %, avec un pic à 16 %. À ces niveaux, nous pourrions être sur le territoire d’un échange de vélos. L'exigence de base du calcul ici est de déterminer si le poids réduit du vélo de route par rapport au vélo de contre-la-montre fait suffisamment de différence sur la vitesse du cycliste pour compenser le préjudice aérodynamique ainsi que le temps nécessaire pour s'arrêter et changer de vélo. Pour résoudre ce problème, nous ferons la somme pour deux coureurs : les poids lourds Filippo Ganna et les poids légers Tadej Pogačar, mais nous devons également faire quelques hypothèses.
Pour nos simulations, nous supposerons que le vélo de route disponible est environ 2 kg plus léger que le vélo aérodynamique et que les deux cyclistes roulent à leur FTP (puissance de seuil fonctionnel) indiqué, et nous utiliserons le poids indiqué par ProCyclingStats. Nous supposerons également un CdA fixe pour les deux vélos/pilotes.
Ainsi, quelques secondes perdues entre les échanges de vélos pourraient laisser un petit avantage. L'avantage simulé est peut-être inférieur à ce à quoi vous vous attendriez, mais notre simulation prend également en compte la réduction de « l'énergie potentielle » due à la masse plus petite.
Pour démontrer une énergie potentielle, préférez-vous être heurté par un train ou une plume roulant à 30 km/h ?
En creusant plus profondément, si nous prenons en compte les pertes aérodynamiques, nous constatons que le vélo de route désavantagera globalement le cycliste, surtout après que les premiers 1,5 km ont été gravis et que la route s'est stabilisée. Nous pouvons rapidement simuler cela pour le savoir.
En supposant que notre cycliste sur un vélo de route ait un CdA fixe de 0,3, alors qu'au-dessus de 20 km/h (c'est-à-dire après la première partie de la montée), notre vélo de contre-la-montre reviendra à un CdA glissant de 0,2.
Dans cette somme, le vélo de route est en retard d'une demi-minute sur la configuration du vélo TT, donc un échange de vélo n'aurait aucun sens. Cependant, les équipes connaîtront plus précisément le CdA, le poids et la puissance de chacun de leurs coureurs sur les configurations de route et de contre-la-montre, ainsi que la rapidité avec laquelle ils peuvent passer d'un vélo à l'autre. Si le détriment du CdA est plus faible ou si la différence de poids est plus grande, cela pourrait alors faire pencher la balance en faveur d'un échange de vélo, en supposant qu'ils puissent le faire rapidement !
Un poids lourd comme Ganna peut-il résister à un poids léger comme Pogacar ?
Cela demande un peu de conjecture quant aux puissances produites ce jour-là. Cependant, nous pouvons constater que ce cours exposera magnifiquement les forces et les faiblesses des deux types de cavaliers. En supposant que les deux utilisent leurs FTP signalés, nous pouvons voir à quel point cela pourrait être proche avec un graphique delta temporel. Vous trouverez ci-dessous une comparaison temporelle simulée entre Ganna et Pogačar.
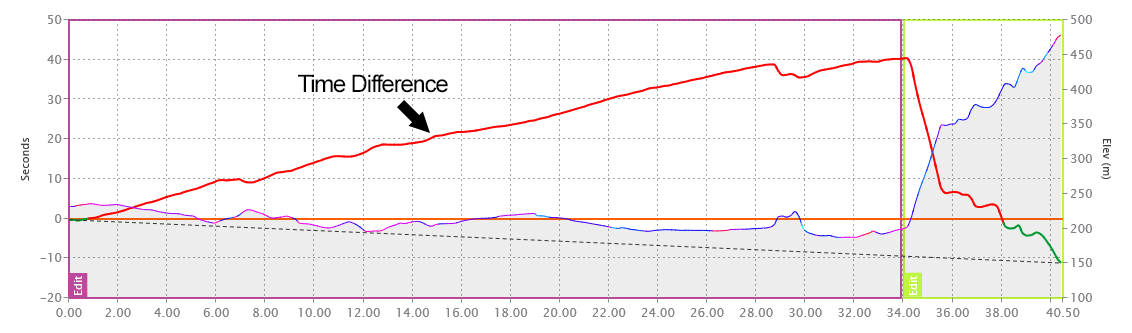
La ligne rouge montre Ganna prenant du temps hors de Pogačar jusqu'au point de contrôle horaire 2. Dans le dernier secteur, Ganna perd rapidement son avantage. Pour que Ganna soit en lice, il doit mener Pogacar de plus de 50 secondes au contrôle horaire 2.
Comme nous l'avons appris plus tôt, il sera payant pour les deux coureurs de « diviser négativement » la course, économisant quelques joules sur le terrain plat avant d'allumer la boîte d'allumettes dans la montée. Il pourrait être difficile pour les coureurs les plus légers d'accepter le déficit de temps aux premiers points de contrôle et de croire que les calculs finiront par être bons.
Ce sera certainement à surveiller.